
Intro
Traditional sensing techniques are demanding of power and bandwidth, meaning that their application is inevitably restricted. New applications – especially in the medical device area of wearable body sensors – require more efficient techniques, and compressed sensing offers a potential solution.
Compressed sensing is based on the principle that, through optimization, the sparsity of a signal can be exploited to recover it from far fewer samples than required by the Shannon-Nyquist sampling theorem. Traditional data acquisition acquires the entire signal at the beginning, then does the compression and throws away most of the information at the end. The new idea combines signal acquisition and compression as one step, which improves the overall sensor design cost significantly.
This new approach opens novel ways for low cost sensor design and ultra-low power hardware processing platforms, not only for biosensors but also areas like image acquisition. Already novel designs have emerged such as the single pixel compressive camera. The camera is capable of obtaining an image using a single detection element (the "single pixel") while measuring the scene fewer times than the number of pixels.
Compressed sensing is a relatively new approach and largely driven by academia. It will take several years and substantial financial investment, but compressed sensing will be key to delivering cost effective eHealth solutions in the next decade.
Compressed Sensing Can Revolutionize eHealth
According to the World Health Organization, cardiovascular diseases are the number one cause of deaths worldwide, responsible for an estimated 17.5 million deaths in 2012 (i.e. 31% of all deaths worldwide) and an economic fallout in the billions.
In order to combat cardiovascular and other diseases, current traditional healthcare infrastructures are increasingly unsuitable due to escalating levels of supervision, medical management, and associated healthcare costs. Data from the OECD show that the U.S. spent 17.1% of its GDP on healthcare in 2013. This was almost 50% more than the next-highest spender (France, 11.6% of GDP), and almost double what was spent in the U.K. (8.8%). A consensus around the need for a cost effective next-generation advanced patient monitoring relies on patient centric eHealth solutions.
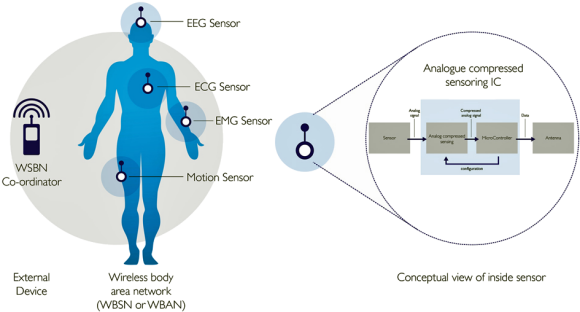
One option is to develop wearable personal health systems based on wireless body sensor networks (WBSN). WBSN-enabled eHealth solutions consisting of outfitting patients with wearable, miniaturized and wireless sensors able to measure, pre-process, and wirelessly report various physiological, metabolic and kinematic bio signals (e.g. ECG, body temperature, SpO2, non-invasive blood pressure) to tele-health providers. This would enable the required personalized, long-term and real-time remote monitoring of chronic patients, its seamless integration with the patient's medical record and its coordination with nursing/medical support.
WBSN are critically resource constrained by limited power supply, memory, processing performance and communication bandwidth. Energy efficiency is necessary in every level of operations (e.g. sensing, computing and transmission) for its successful deployment.
Next page
Understanding Compressed Sensing
Let's start with a simple puzzle that highlights the idea behind compressed sensing. Suppose we have nine pearls, one of which is counterfeit and so of a higher weight than the others. Given an accurate balance scale, can we detect the counterfeit pearl using at most two weighings? The answer is at the end of the article. The puzzle illustrates that when the solution is sparse, i.e., in which most of the elements have the default value, then a reduced number of measurements can be performed and still recover the original solution.
Compressed sensing reconstructs the original signal from a reduced set of measurements in a basis where the signal is known to be sparse. For example, a single tone sine wave is either represented by a single frequency coefficient (sparse in the frequency domain) in the Fourier domain or by an infinite number of time-domain samples.
Any signal can be represented in terms of a basis of vectors as
X = Ψs (1)
Where s is the Nx1 column vector of weighting coefficients and Ψ the NxN basis matrix. As an example, s could be the discrete Fourier coefficients of the signal x while Ψ could be the inverse discrete Fourier matrix. One can make y measurements by taking linear combinations of the signal x as follows:
y = Φx = Φ Ψs = Θs (2)
Where Θ is an MxN sensing matrix with M < N.
The goal of compressed sensing is to design the measurement matrix Θ (note that Θ = ΦΨ) and a reconstruction algorithm for K-sparse (meaning it has k nonzero elements) and compressible signals that require only M=K or slightly more measurements. In this case the system is underdetermined, meaning there is an infinite number of solutions for x. However, the signal is known a priori to be sparse. Under certain conditions, the sparsest signal representation satisfying equation (2) can be shown to be unique. Therefore, sparsity is an important property. The next important property is incoherent sampling. Incoherence means that there is low correlation between any row of Φ and column of Ψ. Random matrices are a good candidate for the sampling matrix Φ as they have low coherence with any fixed basis and as a result the signal basis Ψ.
Signal Reconstruction
The compressed solution is to exploit the prior knowledge on the sparsity of the original signal x. This means that among all possible solutions one is only interested in solutions that are sparse. In general, the sparsity level of the original signal x is not known; therefore the natural way is to find the most sparse solution which satisfies the problem. Then the optimization problem could be written as:
min||s||0 subject to y=Θs (3)
Intuitively, this counts the number of zeros in the vector s, which one wishes to minimize. However, one has to try every 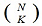 combination of non-zeros to find the solution, which is NP-hard, and thus intractable.
combination of non-zeros to find the solution, which is NP-hard, and thus intractable.
It has been shown that under certain conditions the l1 norm minimization is equivalent to the l0 norm minimization. The l1 norm minimization problem is a convex optimization problem and it can be formulated as a linear optimization problem. Hence, most signal reconstruction algorithms recover s via l1minimization.
min||s||1 subject to y=Θs (4)
Next page
Compressed Architectures
Non-uniform sampler (NUS)
The non-uniform sampler (NUS) is a realization of a compressed sensing system. It is tailored specifically for signals that have a sparse spectrum. The non-uniform sampler acts as an ADC that samples at irregularly spaced intervals. Fourier and time domains are usually extremely incoherent. If the signal x is sparse in frequency then the time samples should be chosen randomly.
What is the advantage of a design like NUS over a conventional ADC? The NUS might take samples spaced at ΔT apart, so at its fastest it still needs to sample at Fs (Nyquist frequency). However, the average sampling rate is M/N.
Its practical applications are widespread including NMR, seismology, speech and image coding, modulation and coding, optimal content, array processing and digital filter design.
Random Demodulator (RD)
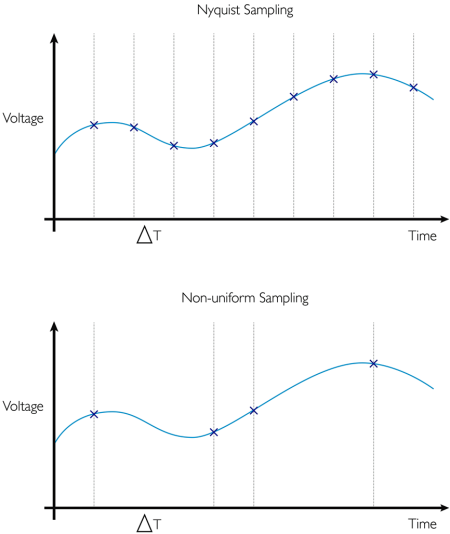
Unlike the NUS sample, the random demodulator samples x at regular intervals below the Nyquist sampling frequency. The first stage is a demodulator whose input signal x is multiplied by a continuous time sequence of pseudo random numbers pc (t) to obtain a continuous time demodulated signal x(t)* pc(t). The pc(t) signal takes values of +/-1 over each frame of N samples and switches between levels randomly at the Nyquist rate of the input signal x.
The final stage is a standard ADC to sample the signal. An integrator (e.g. low pass filter) is used prior to ADC to prevent aliasing. The sampling rate can now be reduced by a factor of m where m is a design parameter. Therefore, the number of measurements M is given by N/m. However, the main disadvantage of the random demodulator is that the coherence of the sensing matrix increases with increasing m.
Next page
Random modulation pre-integrator (RMPI) demodulator
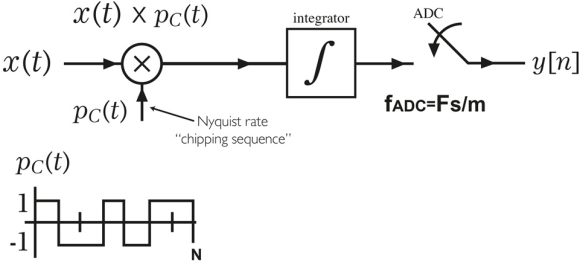
The RMPI is a variant of the RD architecture, which is composed of parallel channels of RD. The continuous time pseudo random signals Pc(t) are chipping signals that take values of +/-1. The alternating frequency of Pc(t) is at the Nyquist rate and the sequences are independent of each channel. The RPMI further reduces the ADC rate by reducing the coherency between rows of the sensing matrix for the same number of measurements compared to the RD architecture. If there are C channels then the number of measurements M is given by C*(N/m).
The RMPI is designed to capture all types of compressible signals. It can also be applied to frequency sparse signals, like the NUS. The cost of this universality, compared to the NUS, is more challenging hardware.
As an example, the Caltech team [1] created a proof of concept design consisting of an eight-channel RPMI device built in CMOS that was designed to capture radar pulses over a 2.5GHz bandwidth.
Spread spectrum random modulator pre-integrator (SRMPI)
A new architecture called SRMPI has been proposed in literature to further reduce the ADC sampling rates. The proposed SRMPI design (like RMPI) is a "universal" encoder, which unlike other architectures (like RM) works with signals that are sparse in any fixed domain.
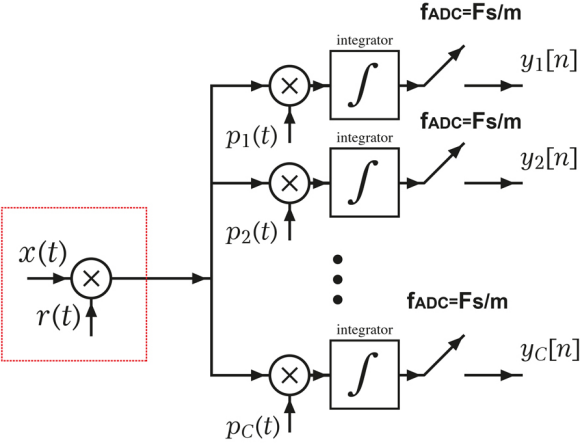
This new pre-modulation block modulates the original signal with a random sequence r(t) similar to in the RD structure. This modulator block should operate at a rate at least equal to Nyquist rate and the information of the signal is thus spread over the whole frequency spectrum. The random-modulated signal is then fed to a regular RMPI structure.
The pre-modulation block signal r(t) makes it possible to lower the internal channel modulators pc(t) working frequency in the SRMPI significantly below the Nyquist sampling rate, therefore reducing overall power consumption. Like with RMPI, if there are C channels then the number of measurements M is given by C*(N/m).
However, the value of m in the SRMPI architecture can be made larger leading to a smaller number of measurements relative to the RMPI architecture. Experimental results in literature [2] indicate that an SRMPI design could reduce power consumption by 75% when compared to the Nyquist rate and by 25% relative to a RPMI design.
Next page
How Compressed Sensing Benefit Sensor Design
- Sensing – By decreasing sampling rates, the ADC power consumption is reduced, as it is approximately proportional to sampling frequency. Sampling at 25% of the Nyquist rate without sacrificing the quality of an ECG signal has been reported [3].
- Storage – By lowering sampling rates, the local storage requirements are reduced.
- Communications – By transmitting fewer samples, the bandwidth requirements are reduced. Therefore, the budget link for the wireless power is decreased.
- Battery – By reducing power requirements, the battery capacity and size are reduced. A 37% extension in the battery life has been reported [3] for an ECG body sensor node.
- Sensor size – By reducing battery size, the overall sensor size is reduced.
- Processing – The reconstruction of the signal can be done on the WBSN coordinator (i.e. outside the sensor) where processing power and electrical power is readily available.
However, the application of compressed sensing to bio-signals is not without challenges. Experiments show that ECG (electrocardiogram) is highly sparse, while EEG (electroencephalogram) and EMG (electromyogram) present less sparsity and are therefore more challenging in the context of compressed sensing.
Conclusion
To date, exploring and designing a low power analog compressed sensing front end for bio-signals has been confined to academia or research institutions. Their designs typically use discrete components (e.g. ADCS, CMOS switches) to realize their implementation, leading to relatively bulky prototypes. For compressed sensing to take off in either mainstream WBSN or active implantables, chip manufacturers will need to package these designs into single "universal" integrated circuits. We believe this will unleash cost effective next-generation advanced patient monitoring systems.
Puzzle Solution: Arrange the nine pearls into three groups of three pearls. Place the first and second group in the balance scales. If the weight is identical then the counterfeit pearl is in the third group. If the weight is different, then the counterfeit pearl is in the group that is the heaviest. Now, we have identified the group that contains the counterfeit pearl. Place one pearl on each balance scales. If the weight is identical then the pearl not weighed is the counterfeit pearl, otherwise it will be the heaviest pearl.
References
[1] http://statweb.stanford.edu/~candes/A2IWeb/rmpi.html
[2] Compressed sensing: a universal energy-efficient compression scheme for biosignals on wireless body sensor nodes, THÈSE NO 6340 (2014), Hossein Mamaghanian http://www.phidiasproject.eu/publications/pdf/EPFL_TH6340.pdf
[3] Compressed Sensing for Bioelectric Signals: A Review, IEEE Journal Of Biomedical And Health Informatics, VOL. 19, NO. 2, March 2015, pp 529-540
About the Author
Dr. Paulo Pinheiro is Head of Electronics, Software and Systems group at Sagentia Ltd. He has a PhD in Three Dimensional Electrical Resistance Tomography from UMIST, UK where he also studied for a Masters in Electrical and Electronic Engineering. Sagentia Ltd is a product development and technology consultancy where he manages a group of electronics, software, and systems engineers.
Related Stories
Wearables Harvest Power From Body Heat
hereO and Flex Collaborate on Development of Location-Enabled Wearables for Families
Unisys Survey Finds Wearable Technology to Revolutionize Biometrics
Temporary Tatts Turn You Into A Remote Control