|
The second part of the question becomes more important when dealing with Web or real-time applications. To answer this question, you?ll have to answer a series of other questions:
- Will it be used in pre- or post-processing, offline analysis, or operator or experimenter?s station input?
- What analytic approach or tool is best suited to your problem or need?
- What is the operational impact on the system from selecting one analytic technique as opposed to another?
- Are there commercial applications (tools) that might help in this application?
The answers to these questions are quite involved and require a lot of thought. This article is written to provide a perspective on these issues and offer insight into the decision-making process.
How Will the Data Be Used?
There are six basic opportunities for analysis: pre-processing, post-processing, online, offline, real time, and non-real-time. Each applies to the time at which the data are analyzed, their relationship to the experiment, and the purpose of the activity. These events can occur simultaneously. Most, if not all, analysis can be defined as some form or combination of the six. The following offers a description of each.
Pre- and Post-Processing Analysis. A test director defines an experiment based on the parameters of interest and the procedure that will capture significant events that detail relationships between the data and the experiment?s hypothesis. The two basic approaches used to extract information from the data are pre- and post-processing.
Pre-processing analyzes the experimental setup and preliminary operational and experimental data prior to initiating the experiment. This ties information and features extracted from the post-processing into the current setup. The results of the analysis bring into focus concerns or issues that must be addressed prior to initiating the experiment and help focus the experiment itself.
Post-processing analyzes data after the experiment has been completed to discover new correlates and information to enhance the knowledge base and to help prepare for the next test in terms of operational activities and needs. Pre- and post-processing are closely linked. The major difference is that post-processing is more specific to discovery while pre-processing is concerned with test preparation and approach. Sometimes it can be difficult to separate the true nature of the two activities, but they are separated by time and intent.
Online and Offline Analysis. Online analysis occurs while a test or process is running. An experimenter?s station or an analysis station collects and analyzes the data and recommends changes in the experiment or process. The data requirements and processing needs are radically different from those of offline analysis. Issues such as acquisition rates, resolution, process time constants, computational requirements, and the user?s interface design make this a challenge. You can use online analysis to verify experimental or process models, extract features, or identify new correlations or events. Also, there?s nothing that precludes you from using it in the discovery mode.
Offline analysis can provide the same data for control, change, and discovery as online analysis?just not as fast and not with the same intent. The difference is that time may not be a dependent variable nor as critical to the process or experiment. This reduces or eliminates the need for computational speed and quick decisions. Because of this, the number and variety of analytical techniques available to you is greater. Where online analysis is concerned with reduced order models (the minimum number of variables and relationships necessary to capture information), offline analysis has the flexibility and latitude to look at all variables (within reason) and to expand the model to include data mining and nonlinear techniques. You still have to consider the impact of models developed offline because they could find their way to online use.
Real-Time or Non-Real-Time Analysis. With real-time analysis, you gather and analyze data at a speed commensurate with the process or experimental dynamics to allow decisions or recommendations to be made in sufficient time to avoid upsetting the stability of the system. Real-time analysis implies that a model of adequate detail has already been developed and that the analysis is focused on determining the state of a system, including its health and off-normal operational modes. For an experiment, it may mean extracting supporting elements for a hypothesis, establishing operational boundaries, or even running a proposed model and letting an algorithm tune it based on a set of constraints. The model could then provide feedback to change the control parameters to get better closure on the model.
Non-real-time analysis assumes that time is not critical. It doesn?t mean, though, that the analysis is being conducted offline and that time is not a dependent variable. It simply means that the results of the analysis?whether that be control, decision making, or model verification?is not critical to the operation of the system.
What Analysis Approach Should I Use?
It may seem confusing, but with some thought, your analytical needs can be mapped onto one, several, or a combination of the six categories discussed here. The actual form it takes will depend on the design of the system, your goal, and what is required üf the analysis. For example, online, real-time analysis will provide an instantaneous look and command of a process or experiment. Online, non-real-time analysis will provide the opportunity to see cause and effect but without the overhead of real-time computing. Offline, real-time analysis will support an experimenter station where feedback is needed to establish new set points for the next steady state equilibrium. Offline, non-real-time analysis provides a more casual setting in which databases can be viewed along with the data set from the experiment (or process) to discern cause and effects or correlates that can be used to determine the steady state operating point.
The importance of the analysis approach you use is based on the impact it has on computational resources and acquisition needs. If these elements aren?t taken into consideration, system performance will degrade significantly, providing less than optimal analytical results. You have only to consider the difference between online, real-time analysis and offline, non-real-time analysis to see the impact.
Online, real-time analysis requires a data acquisition rate commensurate with process dynamics, computational resources available at sufficient levels to analyze the data, and enough compute cycles to effect process changes and decisions. Offline, non-real-time analysis requires only that the system have sufficient computational resources to analyze the data. There?s no overhead for fast data acquisition because the intent is to discover cause and effects or correlates within the confines of resources available to the analysis.
A key discriminator for these systems is the time value of the solution. A real-time, online system needs a timely answer even if it has some associated error (see Figure 1).
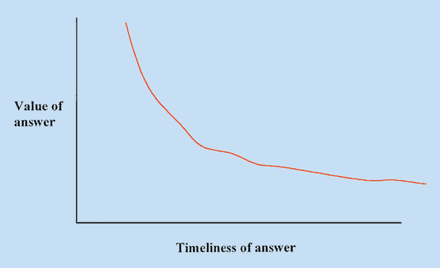 Figure 1. The time value of a solution is characteristic of real-time systems, but it can have a mediating effect on experiments, too. The process time constants determine the time value of the solution, which in turn will have an impact on the system performance and supporting requirements. The exponential curve shown here is just one such time-value function common in real-time systems. Other processes might show a step function, but it will have a declining value, which will be determined by the sensitivity of the process to instabilities. |
Non-real-time and offline analyses don?t have this requirement. Nominally, the ?nswer is to wait until it?s available. In real-time systems, though, you need the answer in time to impact the next step or the answer is of little value.
What Analytic Approach Is Best Suited for My Application?
There?s a wide variety of analytical techniques from which to choose, ranging from the classical statistical and frequency domain techniques to higher order statistical analysis, chaos, and wavelets to model-based techniques to database mining. And unless there are compelling reasons for a particular approach, you can spend an inordinate amount of time selecting the appropriate one.
The following are several of the techniques that are available. It?s not an exhaustive review, but it will give you a feel for the breadth of techniques available to an analyst.
Statistical Methods
Descriptive Statistics. Statistical methods have been around for hundreds of years. It?s an approach where stationary properties of the signal?and not necessarily the dynamic variations?are of interest. The key to using these parameters is understanding that they don?t vary over time. These descriptive statistics include:
- Expected value
- Mean
- Geometric mean
- Variance and standard deviation
- Skew
- Kurtosis
Parametric Evaluations. Many data can be further characterized by their distributions, which include parameter estimates and associated confidence estimates. The distributions include beta, binomial, exponential, gamma, normal, and Poisson. These distributions (which are either discrete or continuous) arise where the experiment dictates which probability distribution may be appropriate for modeling random outcomes.
Linear and Nonlinear Analytic Methods
Linear models are of the form:
| (1) |
where:

You develop this modeling relationship to understand which predictors have the most effect, understanding the track of the observations (increasing/decreasing) and using the model to make the predictions based solely on the predictors. Analytical techniques that support building these types of modeling relationships include multiple linear regression, response surface models, autoregression, moving average, and autoregressive moving average.
Nonlinear regression models are of the form:
| (2) |
There are many nonlinear techniques available for analyzing and extracting features from data. These include chaotic time series analysis, weighted maps, and least squares polynomial methods.
Pattern Recognition
Pattern recognition (or cluster analysis) can be defined as the process by which features are extracted from data, which are, in turn, placed into categories based on some measure of performance, such as minimum Euclidian distance. From these classes, models are developed that relate a data vector to a known pattern or clustering of data. Pattern classification can be in terms of statistics (maximum likelihood functions), error probabilities, and probability density functions. Classifiers can be developed as trainable pattern classifiers. Approaches include the gradient technique and the least mean square error technique. These are good for discovering correlates or relationships in an unsupervised mode.
Spectral Transform Methods
The basic technique for discovering frequency information in time series data is the Fourier transform. This method breaks down a signal into its fundamental (orthogonal) frequency components. The resulting analysis can be used to uncover spectral information described by a linear combination of the contributing frequencies and their relative magnitudes. Included in this group are short-time Fourier transforms and the Gabor expansion.
Other Analytic Methods
There are many other analytic techniques in general use today. These include neural nets, Petri nets, canonical variant analysis, higher order spectral analysis, wavelets, Bayesian forecasting, phase planes, and long-range dependency and self-similarity analysis. Each has a specific purpose and should be investigated before use.
Several of the advanced analytical methods that we?ve used extract features and information from process signals where noise, compounding environmental phenomena, and low SNRs have caused problems for standard approaches. The process dynamics that have been studied with success include arcing across brushes in a 7000 hp motor [1], human physiological impacts from simulator use [2], and micro-bubble cavitation in process flow streams [3].
What Is the Operational Impact on the System?
There are four major design issues [4] that must be addressed when considering the system and the analytical techniques that will be used. They are:
- Scientific and engineering goals
- Ultimate goals and intermediate capabilities
- Budget, scope, and schedule fluctuations
- Overlapping maintenance and development activities
Unless they?re taken into consideration early in the design phase, there will be significant degradation in system performance.
Any scientific mission for the analysis requires more performance than a simple engineering solution. Combining the two in a single system raises significant conflict. Scientific analysis classically places more value on the right answer than on a fast answer. Because many engineering systems are online and real time, they normally place a higher value on the timeliness of the solution, as described earlier.
The ultimate goal versus the intermediate functionality requires careful attention to modularity and scalability. How much faster can I take the samples before I need to discard my entire front end for a faster module? Flexibility costs money, but it?s not as costly as a complete rework. Any online system must, by definition, be able to be upgraded without significant downtime. The upgrades can be hardware or software or both.
Budget, scope, and schedule fluctuations make online systems even more challenging. If the budget gets cut, will the system have reduced capability or will it be useless? Again scalability and modularity are critical. A system that demonstrates early functionality with an architecture that supports modular upgrades has clear advantages in this environment.
Finally, overlapping development, maintenance, and operation (for online systems) will increase system performance requirements. The resources needed to support network access, user interaction, and testing needs during development and maintenance must nýt detract from what?s required for operation. An online system must remain online, even during maintenance and development cycles. Architectures must support parallel processing, shared media, and priority scheduling to make sure that the online, real-time nature of the application is not compromised.
What Software Is Available?
There are many software application programs that provide some level of analysis. Exel and Access have built-in statistical methods. These are basic descriptive parameters. Included in these built-in functions are correlation and cross-correlation techniýues, histograms, and simple plotting routines. For advanced features, you?ll have to consider programs that provide a broader range of analytic techniques as well as graphical representations. These will cover the descriptive to the more advanced techniques, such as wavelets, chaotic times series analysis, and higher order spectral analysis.
Programs that provide the wide range of selections described above include Matlab (Math Works, Inc.), S-Plus (Math Soft), Mathematica ( Wolfram Research), and PV Wave (Visual Numerics, Inc.) to name a few.
References
1. G.O. Allgood and B.R. Upahyaya. April 24-28, 2000. ?A Model-Based High-Frequency Matched Filter Arcing Diagnostic System Based on Principal Component Analysis (PCA) Clustering,? Proc SPIE 14th Annual International Symposium on Aerospace/Defense Sensing, Simulation, and Controls, Applications and Science of Computational Intelligence III, Orlando, FL.
2. G.O. Allgood. April 1991. ?Applications of Advanced Computational Methods for Prediction of Simulator Sickness,? Proc 2nd Annual NASA Symposium on Simulator Sickness, Naval Training Systems Center, Orlando, FL.
3. G.O. Allgood, S.W. Kercel, and W.B. Dress. May 10-12, 1999. ?Developing an Anticipatory Approach for Cavitation?Defining a Model-Based Descriptor Consistent Across Processes,? Proc MARCON 99, Gatlinburg, TN.
4. W.W. Manges. 1986. ?Issues in Developing a Distributed Data Acquisition and Control System,? Proc Eighteenth Southeastern Symposium on System Theory, IEEE Computer Society.
For Further Reading
Chui, Charles K. 1992. An Introduction to Wavelets, Wavelet Analysis and Its Applications, Vol. I., Academic Press.
Maximum Entropy and Bayesian Methods in Applied Statistics. 1986. ed. James H. Justice. Cambridge University Press.
Nonlinear Modeling and Forecasting. 1992. eds. Martin Casdagli and Stephen Eubank. Proc Vol. XII, Reading MA: Addison-Wesley Publishing Co.
Shie Qian and Dapang Chen. 1996. Joint Time-Frequency Analysis Methods and Applications. NJ: Prentice Hall.
Strogatz, Steven H. 1994. Nonlinear Dynamics and Chaos. Reading MA: Addison-Wesley Publishing Co.
Time Series Prediction, Forecasting the Future and Understanding the Past. 1994. eds. Andreas S. Weigend and Neil A. Gershenfeld. Proc Vol. XV, May 14-17, 1992. Reading MA: Addison-Wesley Publishing Co.
Tou, J.T. and R.C. Gonzalez. 1974. Pattern Recognition Principles. Reading MA: Addison-Wesley Publishing Co.
West, Mike and Jeff Harrison. Bayesian Forecasting and Dynamic Models. Springer Series in Statistics, 2nd Ed.
