Wide-ranging measurement methods are applied on the assembly lines of production plants across the country. The ever-rising bar of quality demands rejection of defective products at an assurance level not imagined in years past. The future of defect detection perhaps lies in the identification of assembly line units that are not yet defective, but which could nontheless be expected to fail prematurely in the hands of the consumer.
A production test activity once dominated by mechanically operated micrometers now is characterized by computer controlled measurement devices and data acquisition and analysis systems. Yet, many production plants have not taken advantage of newly developed methods of dynamic measurement and signal processing.
This article addresses dynamic testing as a means of detecting not only on-the-line defects, but also the potential for premature failure after delivery to the customer.
The Dynamic Measurement Concept
It has been found that a large variety of products possess intrinsic dynamic characteristics that provide a signature of the state of their health. Sometimes these characteristics are chemical, optical, electrical, magnetic, or mechanical in nature. There is nevertheless much commonality in the basic measurement and analysis process applied in assessing the state of product health.
The key feature of the dynamic process is the integration of fast, continuous response
 |
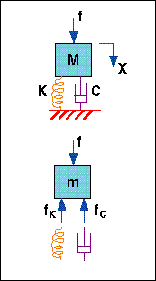| Figure 1. A vibratory force is applied to a simple mass, spring, and damper system (A). The differential equation of motion is developed from the free-body diagram (B). This equation describes the vibration displacement response of the system.HID |
measurement devices, high-speed data acquisition, advanced time and frequency domain signal processing, data analysis, and production line disposition and control. Further, integration on the analysis side should merge statistical analysis methods with techniques of time and frequency domain fingerprinting. While this article focuses on the use of mechanical vibration characteristics for rating product health, the methods described apply as well to measured parameters associated with other kinds of product characteristics.
Single-Degree-of-Freedom
Vibration Theory
Most products, from small to large--from components, computers, TVs, appliances, motors, and equipment to vehicles, aircraft, bridges, and buildings--are rich in vibration characteristics that can indicate their state of health. The reason is that, in a mechanical dynamic sense, these products are all composed of quite a large number of masses, springs, and dampers. And every combination of a mass, spring, and damper has an associated resonance frequency and a mathematical characteristic we call the SDOF FRF (single-degree-of-freedom frequency response function). The combination of many masses, springs, and dampers within a product results in many resonance frequencies, along with the superposition of their FRFs. The FRF resulting from this superposition manifests a myriad of markers useful for assessing product integrity.
The FRF is fundamental to understanding the richness of intrinsic vibration characteristics of a product [1]. It is a mathematical function derived from measurements of an applied dynamic force along with the vibratory response motion, which could be displacement, velocity, or acceleration.
The FRF concept can be understood in association with the simple mass, spring, and damper in Figure 1. A vibratory force, f(t), is applied to the mass, inducing response vibration displacement, x(t). The applied force is typically a random time function having a continuous spectrum over the frequency range of interest. The FRF results from the solution of the differential equation of motion for the SDOF system. This equation is obtained by setting the sum of forces acting on the mass equal to the product of mass times acceleration (Newton's second law):
where:
f (t) = time-dependent force (lb.)
x = time-dependent displacement (in.)
m = system mass
k = spring stiffness (lb.-in.)
c = viscous damping (lb./in./s)
The FRF is a frequency domain function, and we derive it by first taking the Fourier transform of Equation (1). One of the benefits of transforming the time-dependent differential equation is that a fairly easy algebraic equation results, owing to the simple relationship between displacement, velocity, and acceleration in the frequency domain. These relationships lead to an equation that includes only the displacement and force as functions of frequency. Letting F(
) represent the Fourier transform of force and X() represent the transform of displacement:
The circular frequency, v, is used here (radians/s). The damping term is imaginary, due to the 90° phase shift of velocity with respect to displacement for sinusoidal motion. Now the FRF is obtained by solving for the ratio of the displacement Fourier transform to the force Fourier transform. The FRF is usually indicated by the notation, h():
After rationalizing the denominator and defining some key parameters in a more popular form, Equation (3) is written:
 |
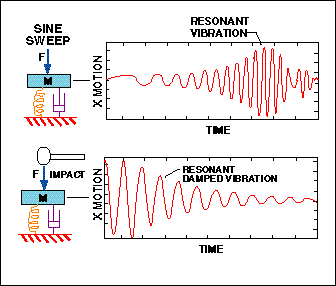| Figure 2. In the vibration response of a single-degree-of-freedom (SDOF) system to two different excitation processes, the upper curve shows response to an applied sine sweep forcing function and the lower curve to a hammer impact force. |
This form of the FRF allows one to recognize the real and imaginary parts separately. The new parameters introduced in Equation (4) are the frequency ratio, 
= / r , and the damping factor, 
. These parameters become clearer upon considering two different ways of inducing vibration on the SDOF system. Figure 2 illustrates the vibration behavior under forced sinusoidal vibration with a continuously increasing frequency compared to vibration resulting from a sudden impact.
The upper diagram of Figure 2 depicts a process in which a computer-controlled electrodynamic shaker impresses a vibration force that slowly sweeps up from a low frequency to a high frequency. The mass and spring respond with amplified vibration as the shaker sweeps into that special frequency range of system resonance. The level of vibration response when forced at the resonance frequency, v r , depends on the amount of damping as quantified by the damping constant, C. The damping factor, , is the ratio of actual damping, C, to the damping value known as critical damping, C c . A system with 
1.0 will not vibrate freely. Typical product values of range from 0.01 to 0.05, except for products specifically designed with high damping, > 0.1, to inhibit vibration.
The lower diagram of Figure 2 reflects that same resonant property of the spring–mass system. The mass and spring are shocked into vibration at the system resonance frequency. The vibration dies away with time at a decay rate dependent on the damping constant, C.
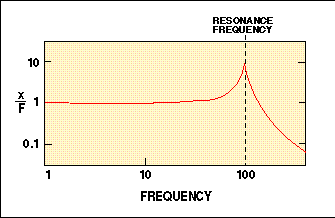
Actually, either of the two displacement-time functions plotted in Figure 2 could be derived from the differential Equation (1). Just enter either the sine sweep forcing function or the hammer impact force for f(t) in Equation (1) and solve for the displacement response. But an efficient use of the data from either of the vibration processes would be to Fourier transform force and displacement measurements and compute the FRF (see Figure 3).
The FRF of Figure 3 directly reflects the sine sweep process. The system response is fairly constant throughout the low-frequency range and rises to a peak at the resonance frequency, r . The resonance frequency can be shown to depend on the system mass and stiffness:
Multiple-Degree-of-Freedom Systems
The reason for this extensive excursion into SDOF vibration theory is that because the most complicated structure, having a large number of masses and springs and resonance frequencies, can be understood as a superposition of simple SDOF systems. Such a complicated system is thought of as a multiple-degree-of-freedom (MDOF) having many modes of vibration. The resulting complicated FRF can be understood as a mathematical summation of SDOF FRFs, each having a resonance frequency, damping factor, modal mass, modal stiffness, and modal damping ratio.
A complicated structure need not have distinct lumped masses and springs to be analyzed as a MDOF system. Product structural elements such as beams and panels represent MDOF components, given their many different modes of bending. Figure 4 summarizes the way in which products may be visualized as a superposition of SDOF modal components, even though lumped masses and springs are not involved. A cantilever beam serves as the example, exhibiting unique deformation patterns called mode shapes. The beam can be made to vibrate freely in any of the individual mode shapes, and, again, associated with each mode shape is a resonance frequency, modal mass, modal stiffness, modal damping, and a modal FRF.
A useful thing to know about vibrating structures is that they can vibrate only using these unique mode shapes. Any arbitrary deformation produced in a vibration process (such as the upper left corner example of Figure 4) can occur only if it is composed of the superposition of the natural mode shapes. This understanding, along with knowledge of the way in which the presence of specific vibrating mode shapes are manifest in measured data, are valuable tools for establishing strategies for product defect detection.
Mode Shape Mathematics
A powerful mathematical concept presents mode shapes as a vehicle for transforming vector components such as displacement, velocity, acceleration, and force from their natural physical coordinate system into an abstract modal coordinate system. A matrix of mode coefficients, 
jr , represents all the mode shapes of interest of a structure. The mode coefficient index, j, locates a numbered position on the structure (a mathematical degree of freedom) and the index, r, indicates the mode shape number. Modes are numbered in accordance with increasing resonance frequencies. The vector component coordinate transformation from abstract modal coordinates, X , to physical coordinates, X, is:
 |
| Figure 3. The frequency response function (FRF) for the SDOF of Figure 1 could be computed from the Fourier transform ratio of X()/F() using data from either of the Figure 2 vibration processes. The FRF peaks at the system resonance frequency, |
Each column in the [] matrix is a list of the mode coefficients describing a mode shape. Figure 4 shows the modal displacements, X 1 , X 2 , X 3 , and X 4 , defined at the end of the cantilever beam for each mode shape. As an example of the coordinate transformation, we see that the physical displacement at position number two, X 2 (see Figure 4, upper left corner), is equal to the sum of the modal displacements weighted by the corresponding mode coefficients.
Now, any system having mass, stiffness and damping distributed throughout can be represented with matrices. Using them, a set of differential equations can be written for the Figure 2 cantilever beam, for example. The frequency domain form is:
Displacements and forces at the numbered positions on the structure appear as elements in column matrices. The mass, damping, and stiffness matrix terms are usually combined into a single dynamic matrix, [D]:
A complete matrix, [H], of FRFs would be the inverse of the dynamic matrix. Thus, we have the relationship:
Individual elements of the [H] matrix are designated with the notation, h jk (), where the j index refers to the row (location of response measurement) and the k index to the column (location of force). A column of the [H] matrix is obtained experimentally by applying a single force at a numbered point, k, on the structure while measuring the response motion at all n points on the structure, j = 1,2,3...n. The [H] matrix completely describes a structure dynamically. A one-time measurement of the [H] matrix defines the structure for all time--until a defect begins to develop. Then subtle changes crop up all over the [H] matrix. From linear algebra we have the transformation from the [ H ] matrix in modal coordinates to the physical [H] matrix.
This provides an understanding of a measured FRF, h jk (), as the superposition of modal FRFs. Equation (10) may be expanded for any element of the [H] matrix (selecting out a row and column) to obtain the result:
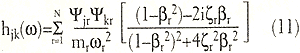
Equation (11) is illustrated graphically in the upper right corner of Figure 4. The solid FRF curve, h 21 , is shown as an algebraic summation of the weighted modal FRFs adjacent to each of the beam mode shapes in the figure. The resonance frequency of each mode of vibration depends on the effective modal mass and effective modal stiffness associated with each SDOF mode shape. The formula for modal resonances is the same as Equation (5):
The modal damping fraction, r , also depends on modal mass and modal stiffness as well as the modal damping constant, c r , because the critical damping value is a function of modal mass and modal stiffness:
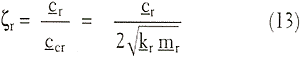
Another useful FRF parameter is the phase angle, indicated by the real and imaginary parts of Equation (11). The phase angle function of frequency, u jk (), associated with FRF h jk () is:
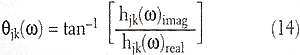
Vibration theory seems overwhelming at times, but the multiplicity of modal parameters within a single FRF can now be appreciated as providing such a rich source of indicators of product health.
Potential Failure Detection
One particularly attractive feature of dynamic defect detection using vibration measurements is the possibility of adjusting rejection criteria for identification of units having statistically significant potential for failure. Mode shape definition, resonance frequency, and the modal damping factor are very sensitive to the mechanical condition of a product--so sensitive, in fact, that is not possible to manufacture two units with precisely identical FRFs. Slight differences between one unit and another will manifest themselves as deviations between their FRFs.
 |
| Figure 4. A cantilever beam exhibits distinct vibration deformation patterns. Each pattern, called a mode shape, behaves like a SDOF component. The measured FRF (upper right corner), X 2 /F 1 , is understood as a superposition of the SDOF FRFs. |
For example, a slightly loosened fastener can affect those mode shapes having large mode coefficients in the vicinity of the fastener. Notice in Equation (11) the effect of mode coefficients on the measured FRF. The loosened fastener will also affect modal stiffness in those modes, changing the resonance frequencies as set forth in Equation (12). Deviations in mode coefficients and resonance frequencies show up as shifts in FRF amplitude, locations of peaks, and phase angle. The damping factor, , may be affected as a result of increased friction in loose joints. This shows up in the FRF as a broadening of peaks as z increases. Figure 5 overlays two FRFs that differ as a result of a slight change in just two of the structure modes. Two mode coefficients have been altered, along with a slight shift in the two resonance frequencies and damping factors.
While an exact theory underlying the relevance of vibration testing to failure potential is not fully developed, the concept is based on fatigue theory. It has been suggested that the fatigue life of certain components can be correlated with their damping factor and resonance frequency. This would mean that the future operating life of some components could be estimated by measuring these modal parameters. On this basis, limits could be established for rejecting units not expected to perform over a normal life span for the product.
Generally speaking, there are two broad defect detection strategies: theory based and phenomenological. The theory-based strategy attacks the problem with full knowledge of the product's dynamic characteristics. The phenomenological strategy uses the same measurement and signal processing methods, but without knowledge of the system model. Both strategies provide the possibility of detecting the potential for premature failure.
 |
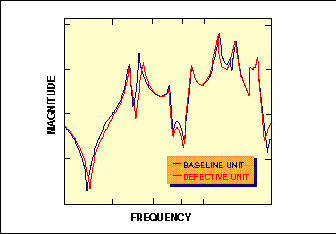| Figure 5. A comparison of FRFs for a baseline unit under test and a defective unit reveals that two modes have been affected by the defect. The results are shifts in resonance frequencies, damping ratios, and mode coefficients. |
Part 2 of this article will take up theory-based and phenomenological defect detection strategies.
Reference
1. Jon Wilson. 1999. "A Practical Approach to Vibration Detection and Measurement, Part 1: Physical Principles and Detection Techniques," Sensors, Vol. 16, No. 2:12-27.
"Part 2: Dynamic and Environmental Effects on Performance," Sensors, Vol. 16, No. 3:52-60.
"Part 3: Installation, Recalibration, and Application," Sensors, Vol. 16, No. 4:46-56.