Wireless sensor networks (WSNs) are becoming more common. They solve problems in many applications, some of which can harvest solar energy to use as a limitless, battery-free energy source. In these applications a supercapacitor provides both temporary energy storage and power delivery. Harvested solar energy can power motion sensors to turn off lights if nobody is detected in a room, to dim lights depending on the light level in a room, to sense and report temperature for air conditioning or heating, and to monitor the security of remote locations while avoiding the need to replace and dispose of batteries.
However, small solar cells are very low power, delivering milliwatts of energy. So the problem becomes how to power wireless transmission, which requires higher amounts of power, using a low-power source.
What Are Supercapacitors?
Supercapacitors are electrical double-layer capacitors. Their electrodes are made of porous carbon and have surface areas >1000 m2/g, providing a huge charge storage area. The electrodes are kept apart by a porous separator that allows ions in solution in the electrolyte to pass through, providing charge transport. The ions rest at the surface of the carbon electrode, so charge separation distance is on the order of nanometers. The size of the charge storage area, coupled with the nanoscale charge separation distance, provides the 'super' capacitance. Key parameters are capacitance (C), Equivalent Series Resistance (ESR), voltage, and volume or weight. Because supercapacitors contain no dielectric, the maximum voltage is determined by the breakdown voltage of the electrolyte. The highest maximum voltage available today is 2.7 V. Supercapacitors are connected in series to achieve higher voltages and a voltage balancing circuit is required to ensure that no individual cell goes overvoltage.
CAP-XX supercapacitors benefit from a nanotechnology construction that packs the highest energy and power densities into thin, prismatic packages that fit space-constrained devices. They store charge on nanoporous carbon electrodes on aluminum foil, arranged in multiple layers, and connected in parallel to minimize the resistance and maximize the capacitance of the device.
Supercapacitors as a Power Buffer
Before there were low-impedance supercapacitors, designers had to size the entire power supply system for the load's peak power. For example, assume a sensor in a remote location is reporting its status once an hour by sensing an SMS that takes 3 s to transmit over a GPRS cellular network. The peak output power during transmission is ~7 W. The average power during the transmission = 7/8 W for 3 s or ~2.6 J. If a capacitor is placed at the input of a buck-boost regulator to allow a wider voltage window—with a maximum voltage of 5 V and minimum voltage of 2.5 V—then input peak power will be ~7 W/85% efficiency or ~8.3 W, and the energy drawn will be ~3 J. To meet these requirements you would require 0.4 F with ESR <50 mΩ, or a supercapacitor. The alternative is to trickle-charge a battery that can deliver this power, possibly with the support of a tantalum or electrolytic capacitor for the 0.577 ms transmission peaks.
The supercapacitor's high energy storage and high power delivery (for CAP-XX supercapacitors these ranges are from 0.5–2 Wh/L and 50–100 kW/L, respectively) allow it to buffer a high-power load from a low-power energy-harvesting source, as shown in Figure 1. The source sees the average load, which with appropriate interface electronics, will be a low-power constant load set at the maximum power point. The load sees a low-impedance source that can deliver the power needed for the duration of the high-power event.
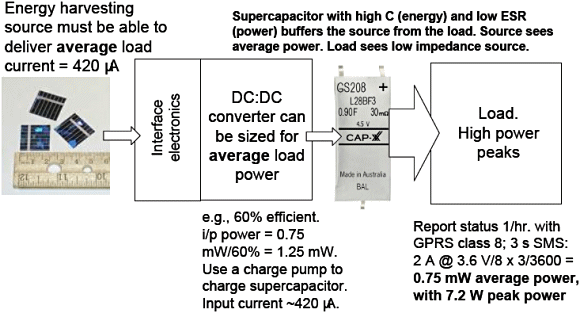 Figure 1. Using a supercapacitor as a power buffer |
In our example, the average load power is 0.75 mW. A low-power solar cell needs to supply a little more than this power level (to overcome losses) to charge the supercapacitor, which then provides the GPRS module with the power required to send the SMS.
The supercapacitor is placed after the interface electronics, allowing designers to size the interface electronics and DC/DC converter for the average power of 1.25 mW rather than the peak power of 7 W. A discharged supercapacitor will look like a short circuit to the source, so the interface electronics must manage the inrush current when the source is first connected to a supercapacitor at 0 V.
Interfacing a Solar Cell to a Supercapacitor
There are four key principles to follow for any circuit that charges a supercapacitor from a solar cell. The circuit should:
- Start charging from 0 V
- Provide overvoltage protection for the supercapacitor
- Prevent the supercapacitor from discharging back into the solar cell when light levels drop
- Be designed for maximum efficiency
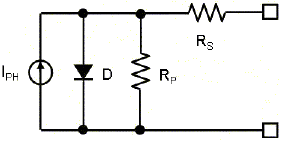 Figure 2. Simplified circuit model of a solar cell |
Figure 2 shows the equivalent circuit of a solar cell. The solar cell generates a current, IPH, that is proportional to the light falling on the cell; if no load is connected then all the current flows through a diode (D), whose forward voltage is VOC. RP represents the leakage current and RS represents connection losses, which are usually not significant. This behavior can be characterized by V- I curves that are provided with the solar cell datasheet. It is useful to characterize the solar cell yourself in the typical light conditions for your application. This can be done by connecting a 10 Ω current sense resistor and a potentiometer across the solar cell, from which you can measure load current and load voltage. The example shown in Figure 3, where the IXYS X0B17 solar cell has been characterized at various light levels, is an array of 3 cells in series.
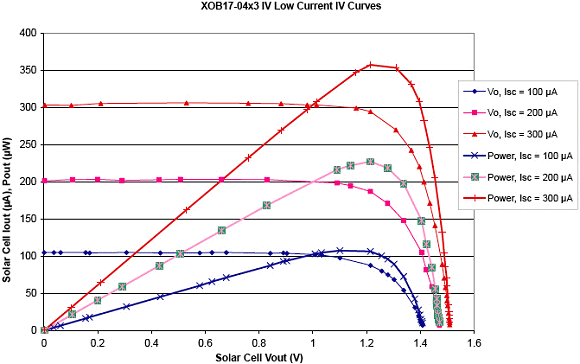 Figure 3. V-I curves for an XOB17 solar cell array |
An important characteristic of solar cells, which makes them easy to connect to supercapacitors, is that they can deliver current into a short circuit or into a discharged supercapacitor. This enables the simple circuit shown in Figure 4. The charging current declines as the supercapacitor charges and the curves from Figure 3 can be used to estimate the charging time for the supercapacitor.
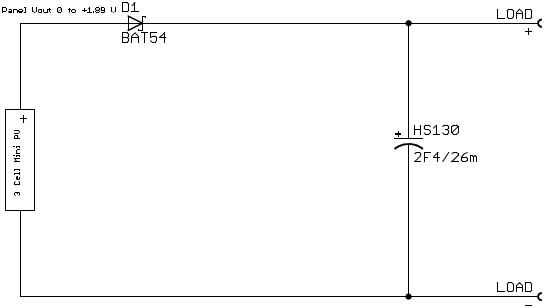 Figure 4. The simplest circuit used to charge a supercapacitor from a solar cell |
The Figure 4 circuit demonstrates several key points:
- VOC of the solar cell at the maximum light levels for the application will be <2.75 V, which will equal the maximum voltage of the single-cell supercapacitor used. This means that the supercapacitor will not require over-voltage protection. Figure 3 confirms this is for the XOB17 solar cell.
- The load can operate at low voltages e.g., the load could be a boost converter with a minimum input voltage of 0.7 V or less (e.g., TPS61200 or MAX1763).
- Diode D1 prevents a charged supercapacitor from discharging back into the solar cell though diode D of the equivalent circuit shown in Figure 2. D1 should be chosen for low reverse leakage current and to minimize the forward voltage drop.
- The supercapacitor should be chosen to deliver the peak-power needs. This constrains the maximum ESR and, because the supercapacitor must support the peak load for its duration, constrains the minimum capacitance. In the circuit shown in Figure 4, we chose the CAP-XX HS130, 2.4 F, 26 mΩ ESR, supercapacitor.
Ideal Supercapacitor Characteristics
The following sections examine the supercapacitor characteristics and circuit requirements necessary to work with a small solar cell.
Low leakage current. If a solar cell provides only a few microamps of current, designers do not want to waste a significant proportion of this on capacitor leakage current. Small supercapacitors have a low leakage current, typically between 1–50 µA, depending on the capacitance and manufacturer. However, this listed value is the equilibrium-level leakage current, achieved after the supercapacitor has been held at voltage for several days. Figure 5 shows the leakage current over time for a 150 mF CAP-XX GZ115 supercapacitor.
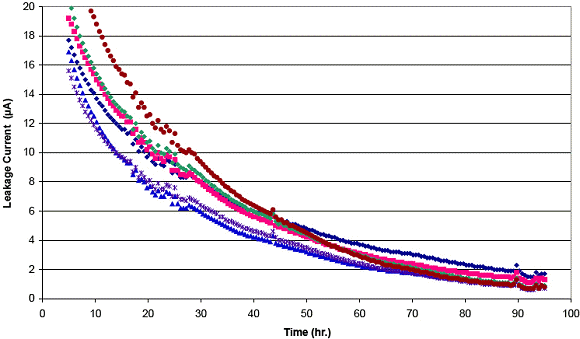 Figure 5. The CAP-XX CZ115 supercapacitor leakage current over time, at 23°C and 2.3 V |
Supercapacitor cell balancing. Supercapacitors are low-voltage devices and therefore several supercapacitor cells need to be strung in series to achieve a practical working voltage. Different cells will have slightly different leakage currents, but because they are in series they must have the same current flowing through them. In this case, the cells will redistribute charge among themselves, i.e., adjust their voltage, so that their leakage currents will be equal. This leaves one of the cells in danger of going over voltage. An active balance circuit draws minimal current by using an ultra-low-current rail-rail op amp. The active balance circuit example in Figure 7 draws 2–3 µA, including supercapacitor leakage current, once the supercapacitor has reached equilibrium leakage current. The MAX4470, which draws ~750 nA supply current, is a suitable op amp for this purpose (U1 of Figure 7).
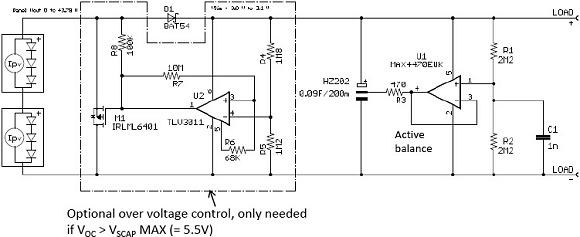 Figure 7. A solar cell-supercapacitor charging circuit with active balancing and overvoltage protection (Click image for larger version) |
Note that in CAP-XX dual-cell supercapacitors, the two cells are matched by capacitance. Because their voltages are balanced when first charged, designers can use a very low-current balance circuit to maintain this balance.
Aging. All supercapacitors age over time, i.e., their ESR slowly increases and their capacitance slowly decreases. The rate of aging depends on the supercapacitor's operating voltage and temperature; the higher the voltage and/or temperature, the faster it ages. Therefore, designers should size the supercapacitor so that the C is large enough and ESR low enough for successful operation at end of life, given the application's expected operating profile. Figure 6 shows capacitance over time for 1 year for a CAP-XX GW214 supercapacitor at 3.6 V and room temperature (23°C).
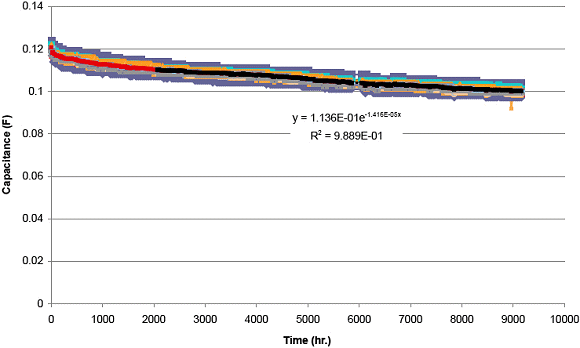 Figure 6. Aging, capacitance loss over time at room temperature (23°C), and ambient RH is 1.4%/1000 hr |
Supercapacitor Interface Circuit Example
The points discussed earlier have been combined into the circuit of Figure 7, where a solar cell charges a dual-cell supercapacitor with active balancing and overvoltage protection. The active balance block on the right is a voltage follower set to VSCAP/2 by R1 and R2, where VSCAP is the voltage across the supercapacitor. Op amp U1 can source / sink up to 10 mA. Op amp U2 turns PFET M1 on when VSCAP > VREF × (R3 + R4)/R3, with hysteresis provided by R6 and R7+R8, so this block acts as a shunt regulator to ensure that the solar cell does not charge the supercapacitor past its maximum voltage. U2 is open drain so that M1 is held off by R8 until VSCAP ≥ 1.8 V and U2 starts to operate. This makes sure the supercapacitor charges from 0 V and the shunt regulator does not operate prematurely.
The charging circuits shown have not taken the solar cell maximum power operating point (MPP) into account. In Figure 3, this occurs when the solar cell voltage is ~1.2 V for the XOB17. This is because designers are better off charging the supercapacitor at ISC from 0 V, rather than reducing the charge current to operate the solar cell near its MPP. As the supercapacitor charges, designers are better off approaching VOC, or the maximum operating voltage for the supercapacitor, whichever is lower, to maximize energy storage. If a boost converter is used to charge the supercapacitor, then the boost converter should be placed where the inductor and forward diode (which may be the body diode of a PFET) provide a charge path with the converter not operating and the circuit should be sized to handle ISC from the solar cell.
Sizing the Supercapacitor
Many people calculate the capacitance required by performing an energy balance shown in Equation 1, where the left-hand term is the supercapacitor energy:
| (1) |
where:
| C | = | capacitance |
| Vinit | = | initial supercapacitor voltage |
| Vfinal | = | minimum voltage that the supercapacitor can discharge at the end of the peak load |
| ELOAD | = | load energy = average load power × load duration |
Therefore, capacitance is given by Equation 2:
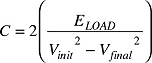 | (2) |
However, this approach ignores ESR and is only a good approximation if the voltage drop from ILOAD × ESR << Vfinal. There are two cases to consider:
Constant current. In this case, the load current is constant and does not vary with voltage, so as the supercapacitor discharges and the load voltage drops, the load current remains constant. An LED is a good example of this type of load. The final load voltage is given by Equation 3:
| (3) |
where:
| ILOAD | = | load current |
| TLOAD | = | the load time of duration |
Now a supercapacitor can be selected with both C and ESR adequate to support the load for duration TLOAD.
Constant power. In this case, the load power remains constant, so as the supercapacitor discharges and the load voltage drops, the load current increases to maintain the VLOAD × ILOAD product constant. The input to a DC/DC converter is a constant power load, so this will be the most common case in energy-harvesting applications. Designers need to solve the following model in Figure 8:
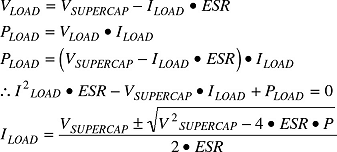 |
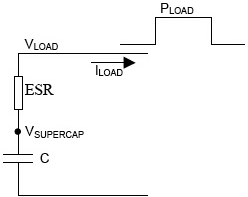 Figure 8. The model for solving the constant power case. Note that VSUPERCAP is not physically measurable, because C and ESR are idealized parameters within the supercapacitor |
Conclusions
Supercapacitors offer an important benefit for solar energy-harvesting applications—the ability to buffer a high-power load from a low-power source in a small form factor—but they do not behave like classical capacitors. This article has explored some key properties of supercapacitors that engineers should understand when designing solar cell circuits, with example circuits that can be used as reference designs and modified for other applications.
ABOUT THE AUTHOR
Pierre Mars, BE electrical (1st class honors), MEng Sc, is the VP of Applications Engineering for CAP-XX (Australia) Pty. Ltd., Sydney, Australia. He jointly holds three patents on supercapacitor applications. The company can be reached at [email protected].
