Linear Hall sensors generate a DC output voltage proportional to the strength of an applied magnetic field and can be used for high-resolution angle sensors when placed near a diametrically magnetized magnet (Figure 1). The rotating magnet generates a sinusoidal waveform, one full wave per revolution. This type of setup can be used only for a limited angular range because the output voltage (in relation to the rotation angle) is ambiguous at angles >90° in both directions from the zero crossing point.
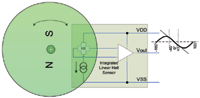 Figure 1. Simple angular measurement using a linear Hall sensor |
In practice, only the "quasi-linear" range up to about ±45° can be used for accurate angle measurements. This setup—being very sensitive to the position of the sensor relative to the magnet and to unwanted external magnetic fields—requires tight mechanical tolerances and, in many cases, magnetic shielding. The temperature of the magnet is also important; magnet strength changes with temperature, resulting in an undesirable output voltage change. To compensate, the Hall sensor must be able to measure the temperature and correct the output voltage according to the temperature coefficient of the magnet.
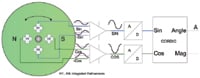 Figure 2. Measurement principle of a 360° Hall-based sensor |
Angle Measurements up to 360°
Making angular measurements over a full revolution requires additional measures. Austriamicrosystems' approach uses four Hall elements, rather than one, and spaces them equally underneath a diametrically magnetized rotating magnet (Figure 2) to generate four sinusoidal waveforms, each phase shifted by 90° from its neighbor, as shown in Equation 1:
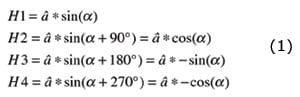 |
where:
â = peak amplitude
α = magnet rotational angle relative to the sensor
By using differential amplification of two opposite sensors (H1–H3 and H2–H4), we get Equation 2, which generates two 90° phase-shifted signals with double amplitude:
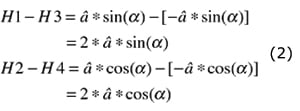 |
These two analog signals are digitized by ADCs and processed further in the digital domain.
The CORDIC Algorithm
A CORDIC (coordinate rotation digital computer) transforms sine and cosine information into angle and magnitude information, using the following relationships:
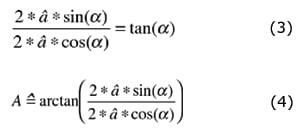 |
where:
A= measured angle
α = magnet rotational angle relative to the sensor
â = peak amplitude
Dividing 2*â*sin(α) by 2*â*cos(α), the remaining expression is shown in Equation 5:
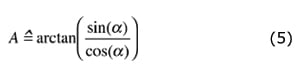 |
This shows the approach's major advantage: it is independent of the signal amplitude and consequently independent of both temperature and vertical-gap variations of the magnet and temperature drift of the Hall elements. It also cancels magnetic offsets caused by external magnetic fields.
Figure 3 shows the arctangent function of Equation 5 over the rotation angle. Depending on the sign of the input signals, sin(α) and cos(α), a linearly increasing output signal can be generated over a full turn of 360°.
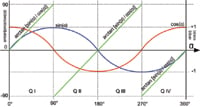 Figure 3. Input and output functions of the CORDIC algorithm |
Depending on the application, the absolute angle information can be converted into further output formats, such as serial, PWM, or analog.
Accuracy of the Encoder System
There are two important parameters, resolution and accuracy, which are not necessarily related to each other. Resolution is the smallest angle step, given as the number of uniformly continuous steps per revolution. For example, a 12-bit encoder has a resolution of 212 = 4096 steps/revolution or 0.08789°/step. Resolution is mainly determined by the resolution of the ADC(s) and the calculation depth of the CORDIC.
Accuracy is the deviation between the indicated angle and the actual angle. Several parameters affect the accuracy and eventually define the quality of an encoder.
Phase error of the Hall signals. At first glance, this parameter doesn't seem to have a large influence, as the Hall elements are spaced exactly 90° from each other. While, in principle, the Hall sensor signals listed in Equation 1 should be phase-shifted by exactly 90°, if the sine and cosine signal paths experience different propagation delays this error can have a substantial influence, especially at high rotational speeds. This effect is even greater when the Hall signals are not available at the same time, for example when only one ADC is used and samples the Hall signals sequentially.
To counteract this, the AS5000 series of magnetic Hall sensors use parallel signal processing (as shown in Figure 2), which keeps the phase error negligible, even at high rotational speeds.
Offset errors in the signal path. Offset errors occur primarily in the Hall element and are due to poor transistor matching of the components in the analog signal path. This error can be tackled by appropriate design methods, e.g., spinning current compensation in the Hall element, chopper amplifiers, and chip trimming.
Matching error of Hall sensors and amplifiers. Trimming can compensate matching errors relatively well but a great deal of effort is required to achieve ideal trimming, especially over the full temperature range. The primary task when designing such a system is to keep these errors as small as possible from the start.
With the above-mentioned error sources, the formula for calculating the angle (Equation 4) changes to Equation 6:
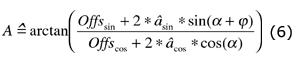 |
where:
A= measured angle
α = magnet rotational angle relative to the sensor
asin = peak sine amplitude
acos = peak cosine amplitude
φ = phase error between sin and cos signal
Offssin = Offset error, sine amplitude
Offscos = Offset error, cosine amplitude
 Benefits of the Integrated Hall Technology |
Nonlinearity of the ADC. ADC nonlinearity cannot be compensated for, so high-performance ADCs are required. The AS504x encoder series from austriamicrosystems is using ΔΣ ADCs, which have excellent linearity.
Nonlinearity of the Magnet. Figure 4 shows a cross section of the sensor and magnet setup from Figure 2. The sensor is sensitive to the vertical magnetic field component. If this component is plotted along the diameter of the magnet, maxima appear at the respective poles near the opposite edges of the magnet. At the neutral zone in the center of the magnet the magnetic field is zero. Magnetic field strength increases relatively linearly with increasing radius.
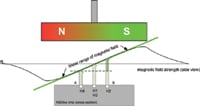 Figure 4. Vertical field distribution of a magnet |
As long as all Hall elements of the array are within this linear range, the differential signals from Equation 2 will remain unchanged and independent of the horizontal position of the magnet. While larger diameter magnets allow more radial misalignment than smaller ones, they have a shallower field distribution curve, resulting in a smaller differential signal. This in turn requires more amplification and results in a poorer signal-to-noise ratio.
Figure 5 shows a typical uncalibrated error curve of a 6 mm dia. magnet at an axial distance of 0.5 mm between magnet and IC, measured with the AS5040 10-bit encoder. The horizontal axes display the lateral misalignment of the magnet in the X and Y directions over a ±1 mm displacement. The center of the bottom square corresponds to a magnet that is perfectly centered over the Hall array. The vertical axis displays the worst-case error over a full turn at each X,Y displacement. As the graph shows, even an imperfectly centered magnet can achieve an accuracy of better than 1°; with a centered magnet, the accuracy is better than 0.5°.
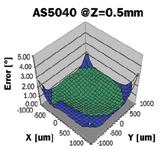 Figure 5. Typical error curve of a 6 mm dia. magnet |
The AS5000 series of magnetic rotary encoders offers a variety of products for different applications, from a low-cost 8-bit encoder to a high-precision, low-noise 12-bit version. The encoders' robustness and contactless measurement principle make them a suitable choice for applications where electromechanical, inductive, optical, or other measurement principles are either too unreliable or too expensive. Their small form factor and low number of external components required (essentially only the magnet and 1–2 decoupling capacitors) allow you to realize precision encoders in small geometries, enabling new sensing applications.
The 360° angle measurement principle introduced in this article is covered by one or more patents registered to austriamicrosystems AG.
Josef Janisch, Dipl.-HTL-Ing, can be reached at austriamicrosystems AG, Schloss Premstaetten, Austria; +43 (0)3136-500-5968, [email protected], www.austriamicrosystems.com.