When you're the CTO of a device networking solution company you spend a lot of time speaking to customers about their respective connectivity challenges and different technology options. Over the past few years, a shift has occurred as a result of two things: the expanded use of wireless technologies and the subsequent desire to connect equipment that has never really been connected before. The blessing of the old wired connectivity days was that you generally always had a way to get power. Sure there might not have been a handy receptacle, but creative minds have come up with ways of sharing wired media such as the legacy 4–20 mA current loop or the more modern power over Ethernet with 802.3AF.
Alas, switching to a wireless data line means that we need to cut the power line as well. This means that we are left with harvesting power from our environment and/or accessing power stored in batteries. As it turns out, the number one question I get asked when speaking with customers about wireless sensor networking is not "which wireless technology should I use?" or "what kind of range will I get?" (although these questions invariably come up), it's "how long will my batteries last?"
The initial answer "well, it depends" is accurate but not comprehensive enough and so this article is intended to start users down the path toward a better answer. It will cover battery vocabulary and two simple but fundamental battery rules. It will also break down different battery technologies and provide a formula for calculating battery life. For my examples, I'll be referring to AA-sized batteries. While almost any size will do, AA batteries are the most common battery size and, because they are readily available in most battery chemistries, they are easy to compare.
A Simple Model
A battery acts like a storage tank. Think of current as the flow out of the tank and voltage as the energy or force behind the flowing liquid. Just like a tank full of water, the energy is greatest when the tank is full and the tank is warm. In batteries, we describe the potential in volts and this voltage tends to decrease as the battery empties.
Overall battery capacity is measured in milli-Amp-hours (mAh) or Amp-hours (Ah). A rating of 3 Ah means the battery can supply 3 A for 1 hour or 1 A for 3 hours. Sometimes the tank is not quite empty, but there is insufficient potential energy in the battery to get the remaining charge out. We tend to say that a battery is empty when the potential or voltage drops below a certain level. Typically, for a 1.5 V cell such as a AA-sized cell, we consider the battery empty when the voltage drops to around 0.9 V.
Now that we are armed with some terminology, it is time to look at two fundamental battery rules.
Battery Rule 1
This first rule relates to temperature. Cold batteries store electricity well, but cold batteries do not supply power well, although some technologies do better than others. With that in mind, it is a good idea to store most batteries in cold places—just make sure to warm them up before use. If you don't warm them up before use, you don't get any of the benefits of cold storage. To extend the storage tank metaphor, it requires more effort to get a cold liquid to flow through a pipe and the same holds true of batteries. Once you use up that energy, you don't get it back.
Battery Rule 2
The second rule relates to the nonlinearity of batteries. The capacity of a battery is related to the current it is being asked to provide. This is not linear. High current draw decreases battery capacity. For example, a battery might have a capacity of 1000 mAh for current draw of 5 mA. However, the same battery might have capacity of 500 mAh for current draw of 200 mA. This is not intuitive to most people but it is very important to understand because most people look at the capacity listed on a battery's spec sheet and assume that it will be linear across varying current draws and temperature. This is a dangerous assumption because it only holds true when the changes in temperature and current are very small.
Now that we are comfortable with battery rules 1 and 2, let's look at different battery technologies. I'll describe their respective behaviors by using a set of simple mathematical models.
Alkaline Batteries
This is the workhorse battery. It is by far the most common type of household battery, and it is very good for a variety of electronics applications, particularly since battery companies have improved the chemistry of the batteries so that they do much better at supplying larger amounts of current. Alkaline batteries are low cost, widely available, and are ideal for low current applications at room temperature. However, they have two major shortcomings: they are terrible in the cold and they don't tend to work as well under high current draws. Figure 1 shows a model of a typical AA-sized alkaline battery at different temperatures and current draws. Notice how the capacity is excellent at low currents and warmer temperatures. We have chosen to model this battery using a second-order polynomial because, for the range of currents in question, a second-order polynomial best represents the nonlinear behavior where total capacity decreases as current draw increases.
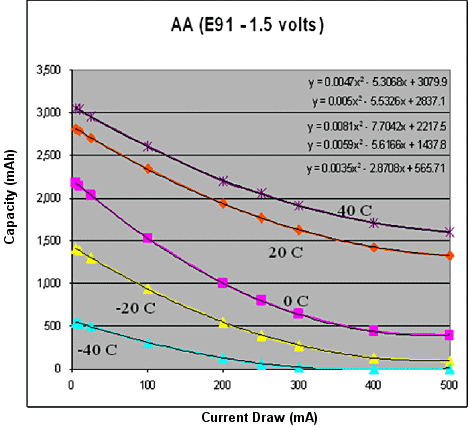 Figure 1. Temperature current model of an alkaline AA battery |
Lithium Batteries
There are many varieties of Lithium batteries. Although it is difficult to put them all in the same class or use the same model to describe their behavior, there are some common characteristics. For the sake of this discussion, we will focus on the iron-disulfide formula in particular because it is the most common Lithium battery available in AA sizes. This type of battery is regularly used as a replacement for alkaline batteries where longer life, higher current draw, or improved temperature performance is needed. Lithium iron-disulfide batteries are not rechargeable (it can be quite dangerous to try to charge one). The big benefit to Lithium disposable batteries is that they do much better under low temperature and high current rate conditions. Figure 2 shows a model of typical AA-sized Lithium iron-disulfide batteries at different temperatures and current draws. Notice how the capacity levels out at higher currents and doesn't do nearly as poorly at low temperatures. The model is clearly not perfect: we must shift the intercept to mitigate the steepness of the initial decline and logarithms of numbers <1 get very negative and very large very quickly. However, we have chosen to model this battery using a logarithmic function to address the somewhat steep decline and quick flattening.
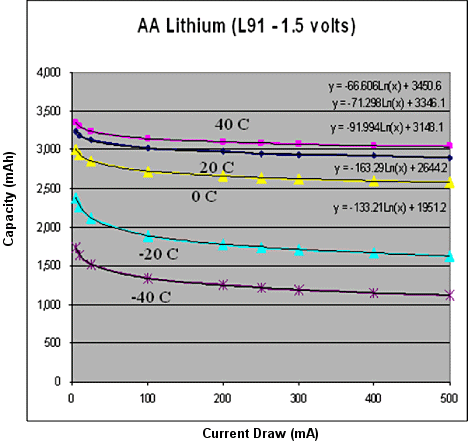 Figure 2. Temperature current model of an AA lithium iron-disulfide battery |
Nickel Metal Hydride (NiMH) Batteries
NiMH is the workhorse of rechargeable batteries. Unlike its cousin, the Nickel Cadmium (NiCAD) battery, it tends to maintain its characteristics through many recharges. Otherwise, it is very similar to Alkaline. Its biggest shortcomings are that it is relatively heavy and that it has a lower energy density, meaning that a typical AA-sized NiMH battery will start at 1.2 V instead of the conventional 1.5 V for an alkaline AA battery. Figure 3 shows a model of a AA-sized NiMH battery for comparison. Its behavior can most easily be described in terms of a second-order polynomial, similar to the model used for alkaline batteries. However, it performs better at low temperatures and doesn't decline quite as quickly as current draw increases.
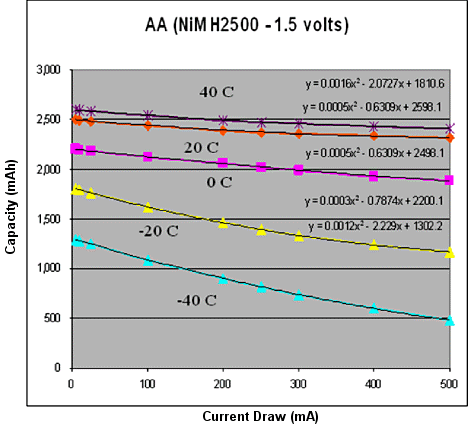 Figure 3. Temperature current model for a AA-sized NiMH battery |
If you want to find models like this for different batteries in general, you can either ask us very, very nicely or create them yourself. We created the aforementioned models by using battery data from spec sheets and then validating various points experimentally. Although no model is ever perfect, and you can never have too much data, we've continued to experiment and collect data.
How to Calculate
Figure 4 illustrates a setup where a temperature sensor is connected to a ZigBee-based network, and then back to a display. The goal is to read the temperature out on the display every minute. Lets assume that each reading transfers 128 bytes of data and that the time to transfer the data, including positive and negative acknowledgements (ACK and NACK) will be about 200 ms.
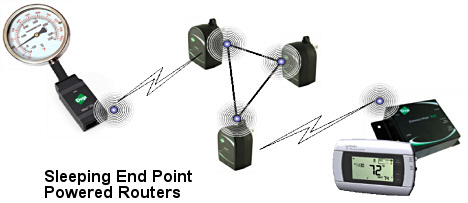 Figure 4. A wireless sensor network setup |
To preserve battery life, the radio must sleep until it needs to transmit or receive data. For the sake of discussion, we'll assume a data transmit and receive time of 200 ms and a wake-up transmit and receive time of 50 ms. The sleep time is whatever is left.
Doing some quick calculations, we see that the awake time and sleep time during the course of a day can be calculated as follows:
Awake Time: 1440 × 250 ms = 360 s (0.1 hr.)
Sleep Time: 86,400 – 360 = 86,040 s (23.9 hr.)
Next we need to ascertain the device's current consumption. Again for the sake of simplicity, assume that the sleep current is 11 µA and the wake-up current is 14 mA. Using these numbers, we calculate our daily energy consumption in mAh as:
Daily Energy in mAh = (11 µA)(23.9)+ (14mA)(0.1) = 1.66 mAh per day
Average Current in mA = 1.66 mAh / 24 hr. = 69 µA
Now to the hard part. For an alkaline battery, we use the AA Alkaline battery model (Figure 5) for an E91 battery.
Figure 5. Alkaline Model (E91 - AA)
| Current: 0.069 mA | Capacity Model for current i in mA | |
| Temperature | Capacity | Output measured in mAh |
| 40°C | 3080 | =0.0047 i2–5.3137 i+3080.8 |
| 20°C | 2839 | =0.005 i2–5.5464 i+2839.1 |
| 0°C | 2217 | =0.0081 i2–7.7065 i + 2217.8 |
| –20°C | 1440 | =0.059 i2–5.6314 i + 1439.9 |
| –40°C | 564 | =0.0035 i2–2.8627 i + 564.55 |
Using these values and plugging in the current consumption (i) and the daily energy consumption we calculated earlier, we have the following:
Temperature of 0°C: 2217 mAh /1.66 mAh = 1335 days
Temperature of 20°C: 2839 mAh /1.66 mAh = 1710 days
If we repeat our calculations for the Lithium battery, and use the model of its behavior in Figure 6, we have the following:
Temperature of 0°C: 2999 mAh /1.66 mAh = 1807 days
Temp of 20°C: 3230 mAh /1.66 mAh = 1946 days
Figure 6. Lithium Model (L91 – AA)
| Current: 0.069 mA | Capacity Model for current i in mA | |
| Temperature | Capacity | Output measured in mAh |
| 40°C | 3342 | = –66.606 ln(i + 5) + 3450.6 |
| 20°C | 3230 | = –71.298 ln(i + 5) + 3346.1 |
| 0°C | 2999 | = –91.994 ln(i + 5) + 3148.1 |
| –20°C | 2379 | = –163.29 ln(i + 5) + 2644.2 |
| –40°C | 1735 | = –133.21 ln(i + 5) + 1952.2 |
Closing Thoughts
We have briefly covered terminology and different battery types and we have looked at the different rules that cause drastic shifts in battery capacity. It is important to understand your objectives before choosing a battery and to take into account current draw and temperature. Remember, you lose battery capacity only once—it doesn't come back.
